#clear all the previous data
rm(list = ls())
#set working directory
#your working directory will be different!
setwd("/Users/dj757/gd/modules/BIO56I/workshops/gwas")
#load the data
load(url("http://www-users.york.ac.uk/~dj757/BIO00056I/data/gwas-data.Rda"))BIO00056I GWAS Workshop
1 Learning objectives
- Understand the principles of quantitative genetics.
- Appreciate how this alters our perspective on evolution.
- Learn how to design experiments that explore quantitative trait variation.
2 Introduction
2.1 Background
In the lectures, we learnt about quantitative traits and how to analyse them. To recap, quantitative traits are often described as complex traits because they are affected by genetic variation in many genes. The genetic variants in those genes each account for a small proportion of the trait variation. We usually assume that they contribute in an additive way (rather than more complex ways).
One good way to identify loci controlling quantitative traits is to perform a genome-wide association study (GWAS). GWAS experiments use diversity panels of individuals to identify genetic markers that are significantly associated with a trait of interest.
Using a diversity panel instead of a biparental mapping population ensures that linkage disequilibrium is low (segments of co-inherited DNA are small), and therefore resolution is high (QTL sizes are small), which helps to narrow down the regions containing the genes controlling the trait. Diversity panels also capture much more genetic variation.
Most traits are quantitative, and are caused by multiple genetic variants. This means that:
- We expect traits to adapt gradually, as a few variants change
- We do not expect to observe many strong selective sweeps
Technical definitions for this workshop.
- Schizosaccharomyces pombe: Fission yeast; a haploid, unicellular fungus widely used as a model organism.
- GWAS: Genome-wide association study; a statistical approach to associate genetic variants with traits across a genome.
- trait: A measurable characteristic (phenotype), such as growth rate at high temperature.
- Manhattan plot: A plot of genomic position (x) versus −log10(P-value) (y) showing association signals across the genome.
- QTL: Quantitative trait locus; a genomic region containing variants that influence a quantitative trait.
- haplotype: A set of genetic variants along a single chromosome that tend to be inherited together.
- selective sweep: Rapid increase in frequency of a beneficial allele, reducing nearby genetic variation via linkage.
2.2 Fission yeast
In this workshop we will use data from the fission yeast Schizosaccharomyces pombe, which is a model species for cell biology. You can read more about S. pombe here.
When fission yeast is not being used in labs as a model species for cell biology, it usually grows on fruit. It is most often found in high-sugar fruits or in fermented beverages (wine, beer, and quite often in cachaça in Brazil).
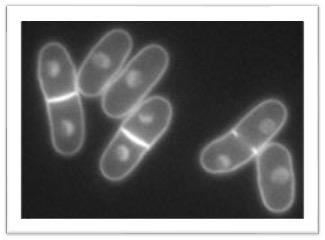
Figure 1. The fission yeast Schizosaccharomyces pombe. Fission yeast is an excellent model system. It is easy to grow in the laboratory, easy to transform, and it has a very small genome (12 Mb). It has ~5,000 protein-coding genes and ~1,500 non-coding RNAs. It is haploid. Fission yeast and the budding yeast Saccharomyces cerevisiae are not closely related fungi, so study of both has contributed greatly to our understanding of molecular biology, evolutionary biology, and quantitative genetics.
2.3 GWAS for yeast
GWAS is often used for human or crop traits, but we can apply this method to any sexually recombining eukaryotic species for which we have trait data and polymorphism data (e.g., SNPs).
The data we will use come from two papers: Nature Genetics and Nature Communications. These articles described the genetic diversity of 160 strains of this species by sequencing their genomes, and measured over 200 traits.
In this workshop we will examine GWAS results for four traits and consider what they could mean for the evolution of this species.
2.4 The traits
The traits we will look at today are:
Growth in 400 mM NaCl The growth rate of the strains in 400 mM salt. This could be important if strains grew in fruit near the sea or in salty substrates.
Growth at elevated temperature The growth rate of the strains at 40 °C. This is quite warm for this yeast, so it is a stressful condition.
Maximal cell density in rich medium This trait measures how well each strain grows when given plenty of sugar and other resources.
Glucose/fructose utilisation in wine How much of the glucose and fructose each strain used in grape must (used to make wine).
A high value in one of these traits could be adaptive in one environment but suboptimal in another. Also, optimising one trait may limit another trait. This could be because one mutation results in multiple changes, or the alleles that influence two traits are closely linked.
3 Exercises
3.1 Exploring the data
First, clear all the previous data you may have in R, set your working directory, and load the GWAS data.
To set a working directory you can either use a command (as below), or use the menus;
Session > Set Working Directory > Choose Directory.
After loading these data you will have four data frames called gluc, heat, rich, and salt. Each contains the GWAS results for one trait. Start by looking at salt.
Try these commands to see what they contain:
#examine what is in the salt data frame
head(salt)
nrow(salt)
summary(salt)
View(salt)This table contains the output from a GWAS tool called LDAK. This is one of many software tools that run GWAS analyses. It describes the association of each SNP with the trait of salt tolerance.
Each row of the table contains information about one SNP. For our purposes, the important columns are:
Wald_P, the P-value, the probability that this SNP is associated with this traitChr, which chromosome the SNP is onBP, the position of the SNP in the chromosomeEffect_size, how strongly this variant affects the trait
The effect size of the variant estimates the proportion of trait variation that is explained by this SNP. From our understanding of the Neutral Theory of Molecular Evolution, we know that most variants are selectively neutral, i.e., they have little or no effect on fitness.
Given this, we might expect that most variants have small, or no, effects on traits.
3.2 Manhattan plot
A Manhattan plot is a standard way of viewing GWAS results. They are named Manhattan plots because they resemble the skyline of a high-rise city, such as Manhattan (New York).
Manhattan plots show the position of the SNP on the x-axis, and the P-value of the association on the y-axis. P-values are plotted as −log10(P), so that very small P-values end up at the top of the plot and stand out.
The code below will make a Manhattan plot for the salt trait.
#set plotting parameters
layout(matrix(c(1:3), 1, 3, byrow = TRUE),widths = c(5579133,4539804,2452883))
par(bty="l",cex=0.8,mar=c(2,2,2,0)+2)
#loop through chromosomes 1,2,3, plotting each one in turn
for (j in 1:3){
#make a subset of SNPs from this chromosome
temp = subset(salt, Chr == j)
#plot these
plot(temp$BP, -log10(temp$Wald_P),
main = paste("Chr",j),ylim=c(1,10),
xlab="position",ylab="-log10(P)"
)
#draw a threshold line
#SNPs above this line are statistically associated with the trait
abline(h=-log10(1e-5),col=2,lty=2)
}- Where are the strongest association signals located (do peaks cluster on particular chromosomes)?
- Why are most points close to the bottom of the plot? What does this tell you about polygenic traits?
- How does the −log10(P) scale aid interpretation compared to plotting raw P-values?
- What biological processes could lead to a few tall peaks versus many low signals (e.g., selection, drift, mutation rate, linkage)?
You will usually see a small number of very low P-values; with large −log10 values they sit at the top of the y-axis. For these, there is strong support that they affect the trait.
You will also see many SNPs with P-values around 0.1 or greater. These are at the bottom of the y-axis. There is weak support that they affect the trait. These may have tiny effect sizes, or none at all.
Note that we use plot(temp$BP, -log10(temp$Wald_P)) to plot the Wald_P P-values on a negative log scale. This means that very significant P-values (e.g., P = 1 × 10^−9.5) will show as high points on the plot (e.g., at position 9.5 on the vertical y-axis in this case).
All the non-significant SNPs (e.g., P = 0.1, which is 1 × 10^−1) will be at the bottom of the y-axis. If most variants have small or no effects on traits, there will be many of these.
This illustrates polygenic architecture: many variants with small effects and a few with larger effects.
3.3 SNP effect sizes
The strength of the association between genotype and phenotype relates to the effect size (how strongly the variant affects the trait). Some alleles affect the trait strongly; most do not. Now make a histogram of all the effect sizes.
hist(salt$Effect_size,br=30)- What does the histogram shape tell you about the distribution of SNP effect sizes?
- How does this pattern relate to the Neutral Theory (many neutral or near-neutral variants)?
- Where would you expect to see evidence of purifying selection or positive selection in such a distribution?
3.4 How does this influence evolution?
Effect size here is the proportion of phenotypic variance explained by that SNP. Most effect sizes are very small—often < 0.05—meaning each explains far less than 5% of the trait variance.
Consider how such tiny-effect alleles influence evolutionary change.
A selective sweep is a process where a beneficial mutation becomes fixed in a population rapidly, removing the genetic variation around the selected allele.
- If a trait is influenced by a few large-effect mutations, how likely is a classic selective sweep and why?
- If a trait is influenced by many tiny-effect mutations, what evolutionary pattern replaces a sweep? (Think subtle allele frequency shifts.)
- How can tight linkage to a deleterious allele modify or slow a sweep?
- What genomic signatures (e.g., reduced diversity, extended haplotype homozygosity) would differ between oligogenic and highly polygenic adaptation?
3.5 Another trait: glucose & fructose use
In a vineyard environment, it is advantageous to metabolise glucose and fructose in rotting fruit. Glucose/fructose use is in the gluc data frame.
Again, we will look at the P-values (Wald_P) and how much each SNP is predicted to affect the trait (Effect_size).
#set plotting parameters
layout(matrix(c(1:3), 1, 3, byrow = TRUE),widths = c(5579133,4539804,2452883))
par(bty="l",cex=0.8,mar=c(2,2,2,0)+2)
#loop through chromosomes 1,2,3, plotting each one in turn
for (j in 1:3){
temp = subset(gluc, Chr == j)
plot(temp$BP, -log10(temp$Wald_P),
main = paste("Chr", j, "Gluc"),ylim=c(1,10),
xlab="position",ylab="-log10(P)"
)
abline(h=-log10(1e-5),col=2,lty=2)
}
::: callout-tip
# Discussion points: second trait comparison
- Do the strongest glucose/fructose association peaks overlap with salt peaks? What could shared loci imply (pleiotropy vs linkage)?
- Are there trait-specific peaks? What might that say about specialised metabolic pathways?
- How could environmental context (salinity vs sugar availability) shift which alleles are favoured?
:::
Again, you will see a small number of very low P-values at the top of the y-axis (strong support) and many higher P-values at the bottom (weak or no support; tiny or no effect sizes).
Now, make a histogram of the effect sizes:hist(gluc$Effect_size)3.6 Looking at two traits
Species cannot adapt to a single condition (e.g., heat or salt) in isolation because environments are complex and variable. As a thought experiment, we will consider this using the fission yeast data.
We will compare two Manhattan plots by overlaying them: salt (black) and glucose/fructose metabolism (red). The output PDF will appear in your working directory.
#open the pdf writer
pdf("GWAS-plot3.pdf",width=60)
#set up the plot layout
layout(matrix(c(1:3), 1, 3, byrow = TRUE),widths = c(5579133,4539804,2452883))
par(bty="l",cex=0.8,mar=c(2,2,2,0)+2)
#loop through chromosomes
for (j in 1:3){
#plot the salt GWAS points (black dots)
temp = subset(salt, Chr == j)
plot(temp$BP, -log10(temp$Wald_P),main = "",ylim=c(1,10),xlab="position",ylab="-log10(P)")
#add the glucose/fructose GWAS points (red crosses)
temp2 = subset(gluc, Chr == j)
points(temp2$BP, -log10(temp2$Wald_P),main = "gluc",ylim=c(1,10),xlab="position",ylab="-log10(P)",col=2,pch=3)
#add the significance threshold
abline(h=-log10(1e-5),col=2,lty=2)
}
#close the pdf writer
dev.off()Now find the pdf called GWAS-plot3.pdf and take a look.
3.6.1 Might mutations for two traits conflict?
Look at the significant peak on chromosome 3 (~1,500,000 bp). This likely has a relatively large effect size. There is also an important variant for glucose/fructose use nearby on chromosome 3.
Consider what might happen if alleles are linked and the environment is complex—salty yet fructose-rich (e.g., a coastal vineyard).
What might happen if helpful alleles for both traits are on the same haplotype?
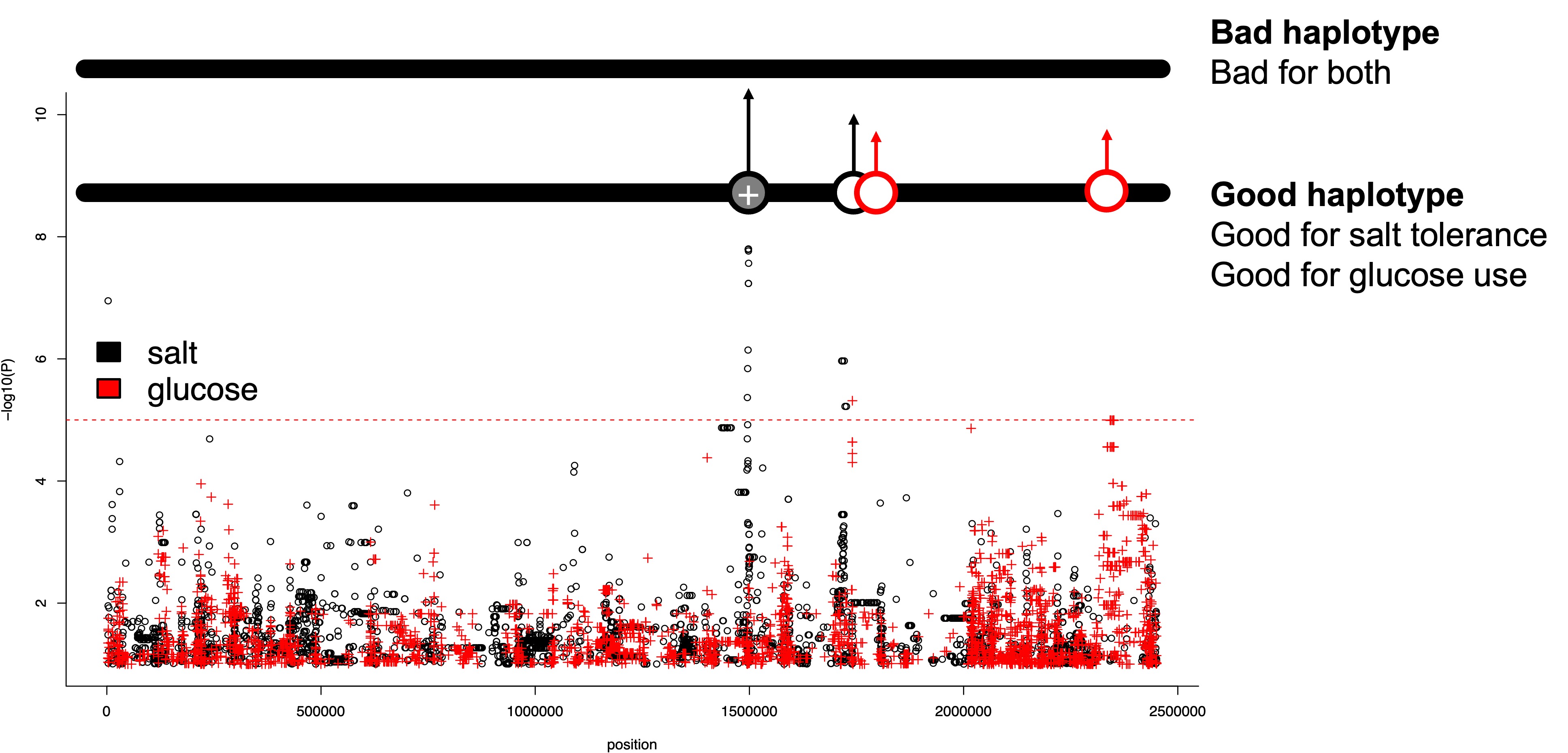
Physically, a haplotype is a stretch of DNA from one chromosome. In diploids, each individual carries two homologous chromosomes. In haploid S. pombe, different haplotypes are simply different chromosome versions present across the population. Through meiotic recombination haplotypes mix, but SNPs very close together rarely separate, so they tend to travel together.
3.6.2 Haplotype problems
Consider these situations:
- What might happen if helpful alleles are on the same haplotype?
- What might happen if helpful alleles are on different (opposing) haplotypes?
The figures below will help to explain.
- How does tight linkage between beneficial alleles influence the speed of joint adaptation?
- What evolutionary constraint arises when beneficial alleles are on different haplotypes in low recombination regions?
- How can recombination rate modulate the resolution of this “conflict” between opposing haplotypes?
- Which scenario (single vs opposing haplotypes) better facilitates rapid multi-trait optimisation?
 Figure 2. Beneficial alleles on one haplotype. Would there be any conflict here?
Figure 2. Beneficial alleles on one haplotype. Would there be any conflict here?
 Figure 3. Beneficial alleles on two different haplotypes. What might happen here? What is the potential problem?
Figure 3. Beneficial alleles on two different haplotypes. What might happen here? What is the potential problem?
4 Summary: what we have learned
This workshop used data from fission yeast, but the principles apply broadly to quantitative traits. Key points:
- Most SNPs do not strongly associate with traits.
- Most SNPs have very small effects on traits, but some do have detectable effects.
- SNPs do not affect all traits at once. Some SNPs affect one trait; some affect another.
- Genetic variants, like SNPs, travel through time and space in haplotypes.
5 After the workshop: exam-style questions
Exam questions often ask you to apply workshop principles to other species or scenarios. Reflecting on these helps deepen understanding.
- Most SNPs have no effect, or very small effects, on traits.
- SNPs that do affect traits are generally responsible for less than 5% of the trait variation.
- Effect sizes are also small for other genetic variants, such as transposon insertions, duplications/deletions and so on.
- Genetic variants can affect one trait, or several.
- In the short term, selection occurs on haplotypes, but over time recombination will separate linked variants.
5.1 Question 1 (10 points)
This question checks your understanding of quantitative traits and why most variants have small effects.
Define the difference between a simple (single-gene) trait and a quantitative trait. Give one example of each from this workshop. (2 points)
The histogram of SNP effect sizes for the salt trait is heavily skewed towards zero. Describe what this pattern tells us about the distribution of SNP effects in the population. (3 points)
Using the Neutral Theory of Molecular Evolution, explain why most SNPs are expected to have little or no effect on fitness. (3 points)
Suggest one practical way to increase the power of a GWAS to detect very small-effect variants and explain why it helps. (2 points)
5.2 Question 2 (10 points)
You notice that the Manhattan plots for salt tolerance and glucose/fructose utilisation share a peak on chromosome 3, but also have trait-specific peaks.
Describe what an overlapping peak for both traits suggests about the underlying genetics of those traits. (3 points)
State one additional analysis you could carry out to test whether the same causal variant influences both traits. (2 points)
Explain how recombination could help resolve a situation where beneficial alleles for two traits are on different haplotypes. (3 points)
Identify one environmental measurement you would collect alongside the genomic data to interpret potential trade-offs between the two traits, and justify your choice. (2 points)